Adaptive Range Market Maker (ARMM)

A Next-Generation Approach to Decentralized Liquidity Provision

Abstract

This paper introduces the Adaptive Range Market Maker (ARMM), a novel automated market maker protocol that addresses the fundamental challenges of capital efficiency, impermanent loss, and price discovery in decentralized finance.

Traditional automated market makers have served DeFi well, but their limitations in capital efficiency and risk management have become increasingly apparent. Today, we're excited to introduce the Adaptive Range Market Maker (ARMM), a revolutionary approach to on-chain liquidity provision.

ARMM reimagines market making through its innovative multi-band liquidity system. Unlike traditional AMMs or DLMMs that use a single pricing curve, ARMM deploys capital across multiple, autonomous liquidity bands. Each band operates with its own risk profile and strategy, similar to how traditional finance employs multiple trading desks with different mandates. This approach draws from our experience running proprietary trading desks in the traditional finance industry.

2. Technical Architecture

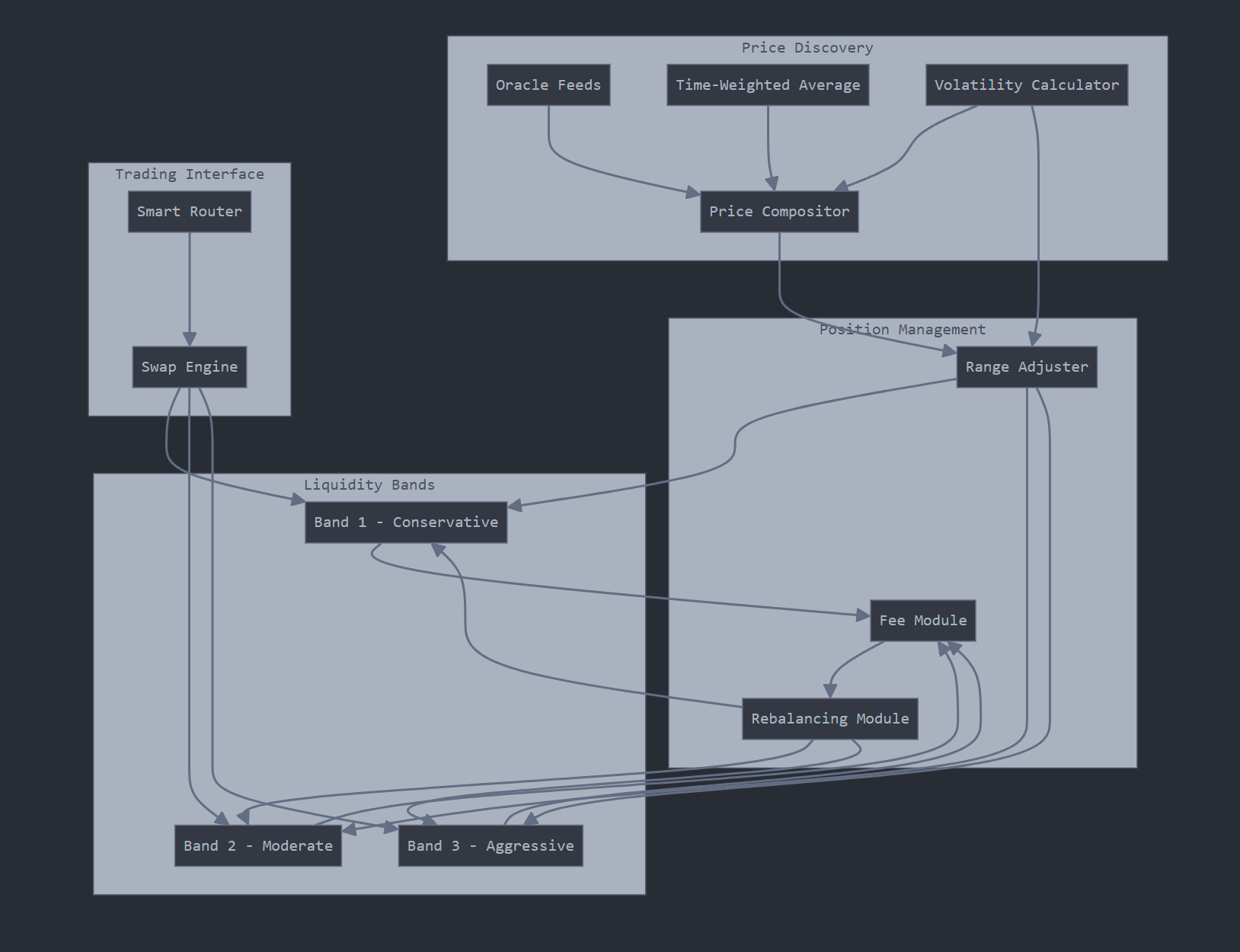
2.1 Core Components

The ARMM protocol consists of four primary systems:

2.1.1 Band Management System (BMS)

struct LiquidityBand {
    uint256 baseAmount;
    uint256 quoteAmount;
    uint256 lowerPrice;
    uint256 upperPrice;
    uint256 volatilityMetric;
    uint256 utilizationRate;
}

The BMS manages multiple overlapping liquidity bands, each operating with independent parameters optimized for different market conditions and risk profiles.

2.1.2 Price Discovery Engine (PDE)

struct PricePoint {
    uint256 timestamp;
    uint256 price;
    uint256 confidence;
    uint256 volume;
}

The PDE aggregates data from multiple sources, including:

• External oracle feeds
• Time-weighted average prices (TWAP)
• Volume-weighted average prices (VWAP)
• On-chain orderbook data

2.1.3 Position Management System (PMS)

struct PositionMetrics {
    uint256 impermanentLoss;
    uint256 feeRevenue;
    uint256 utilizationRate;
    uint256 profitability;
}

The PMS optimizes position sizing and placement across bands based on real-time market conditions and historical performance data.

2.1.4 Risk Management Framework (RMF)

struct RiskParameters {
    uint256 maxDrawdown;
    uint256 volatilityThreshold;
    uint256 liquidityConstraints;
    uint256 concentrationLimits;
}

3. Economic Model

3.1 Dynamic Fee Structure

The protocol implements a multi-tiered fee system:

function calculateFee(
    uint256 tradeSize,
    uint256 bandIndex,
    uint256 volatility
) public view returns (uint256) {
    return baseFee
        .mul(utilizationMultiplier())
        .mul(volatilityMultiplier(volatility))
        .mul(sizingMultiplier(tradeSize));
}

3.2 Liquidity Provider Incentives

LPs receive rewards through:

• Trading fees proportional to their capital contribution
• Band-specific yield based on utilization rates
• Bonus rewards for optimal band placement
• Risk-adjusted returns based on volatility exposure

4. Risk Mitigation

4.1 Impermanent Loss Protection

ARMM implements several mechanisms to reduce IL:

• Autonomous range adjustment based on volatility predictions
• Cross-band rebalancing to optimize position distribution
• Optional IL insurance through integrated options protocols

4.2 Smart Contract Security

The protocol employs multiple security layers:

• Formal verification of core contracts
• Rate limiting on parameter adjustments
• Emergency shutdown mechanisms
• Graduated access controls

5. Governance and Parameter Optimization

5.1 Parameter Adjustment

Key protocol parameters are managed through:

• On-chain governance
• Automated adjustment mechanisms
• Risk-weighted voting systems

5.2 Governance Structure

The protocol implements a two-tiered governance system:

• Technical parameter adjustment through algorithmic control
• Strategic decisions through token-holder voting

6. Future Developments

6.1 Planned Enhancements

• Cross-chain liquidity aggregation
• Advanced derivatives integration
• Layer 2 scaling solutions
• Enhanced oracle networks

6.2 Research Directions

• Machine learning for parameter optimization
• Game theory modeling for LP incentives
• Advanced risk management algorithms

7. Conclusion

ARMM represents a significant advancement in AMM design, offering improved capital efficiency, reduced impermanent loss, and enhanced adaptability to market conditions. Through its innovative multi-band system and dynamic parameter adjustment, ARMM provides a robust foundation for the next generation of decentralized trading protocols.

Key Components and Innovations:

1. Advanced Band Management System:

contract ARMMBandManager {
    struct BandMetrics {
        uint256 utilization;        // Current capital utilization
        uint256 profitability;      // Historical profit metrics
        uint256 impermanentLoss;    // IL tracking
        uint256 volatilityScore;    // Local volatility measure
    }

    // Dynamic band adjustment parameters
    struct BandParameters {
        uint256 targetUtilization;  // Optimal capital usage
        uint256 maxVolatility;      // Volatility threshold
        uint256 rebalanceThreshold; // Trigger for rebalancing
        uint256 feeMultiplier;      // Dynamic fee adjustment
    }
    
    function optimizeBand(uint256 bandIndex) internal {
        BandMetrics memory metrics = calculateBandMetrics(bandIndex);
        BandParameters memory params = getBandParameters(bandIndex);
        
        // Adjust band width based on metrics
        if (metrics.volatilityScore > params.maxVolatility) {
            narrowBand(bandIndex);
        } else if (metrics.utilization > params.targetUtilization) {
            expandBand(bandIndex);
        }
        
        // Optimize fee structure
        adjustFees(bandIndex, metrics, params);
    }
}

2. Volatility-Aware Pricing Engine:

contract ARMMPricing {
    struct PricePoint {
        uint256 timestamp;
        uint256 price;
        uint256 confidence;    // Confidence score based on source
        uint256 volume;        // Trading volume at this price
    }
    
    function calculateOptimalPrice(
        PricePoint[] memory prices,
        uint256 timeWindow
    ) public view returns (uint256) {
        // Weight recent prices more heavily
        uint256 timeDecay = calculateTimeDecay(timeWindow);
        
        // Consider volume-weighted average
        uint256 vwap = calculateVWAP(prices);
        
        // Include confidence-weighted components
        uint256 confidenceWeight = calculateConfidenceMetric(prices);
        
        return computeFinalPrice(vwap, confidenceWeight, timeDecay);
    }
}

3. Intelligent Capital Allocation:

contract ARMMCapitalManager {
    struct CapitalAllocation {
        uint256 activeCapital;      // Currently deployed
        uint256 reserveCapital;     // Ready for rebalancing
        uint256 hedgingCapital;     // Used for IL protection
    }
    
    function optimizeCapitalAllocation(
        uint256[] memory bandUtilization,
        uint256[] memory profitMetrics
    ) internal returns (CapitalAllocation[] memory) {
        // Calculate optimal distribution
        uint256 totalCapital = getTotalCapital();
        uint256[] memory allocation = new uint256[](bandUtilization.length);
        
        // Consider cross-band relationships
        for (uint256 i = 0; i < bandUtilization.length; i++) {
            allocation[i] = calculateOptimalAllocation(
                bandUtilization[i],
                profitMetrics[i],
                totalCapital
            );
        }
        
        return executeReallocation(allocation);
    }
}

4. Risk Management System:

contract ARMMRiskManager {
    struct RiskMetrics {
        uint256 shortTermRisk;      // Immediate market risks
        uint256 systemicRisk;       // Protocol-level risks
        uint256 counterpartyRisk;   // Trading partner risks
    }
    
    function assessRiskLevel(
        uint256 bandIndex,
        uint256 tradeSize
    ) public view returns (uint256) {
        RiskMetrics memory metrics = calculateRiskMetrics(bandIndex);
        
        // Combine different risk factors
        uint256 riskScore = metrics.shortTermRisk
            .mul(getVolatilityImpact())
            .add(metrics.systemicRisk)
            .add(calculateTradeImpact(tradeSize));
            
        return adjustPositionLimits(riskScore);
    }
}

The ARMM system introduces several key innovations over existing AMMs:

1. Predictive Liquidity Positioning: Instead of reactive adjustments, the system anticipates market movements using its volatility and price feed data.

2. Risk-Adjusted Returns: Each liquidity band operates with its own risk profile, allowing LPs to choose their preferred risk-return tradeoff.

3. Dynamic Capital Efficiency: The system automatically redistributes capital across bands based on market conditions and trading opportunities.

4. Smart Fee Optimization: Fees adjust based on band utilization, market volatility, and trading patterns to maximize LP returns while maintaining competitive pricing.

Let me create a practical example comparing how DLMM and ARMM would handle a real-world trading scenario. This will help demonstrate the key advantages of ARMM's architecture.

Scenario: Let's consider an ETH/USDC pool with $10M in total liquidity during a period of increasing market volatility.

First, let's visualize how both systems work:

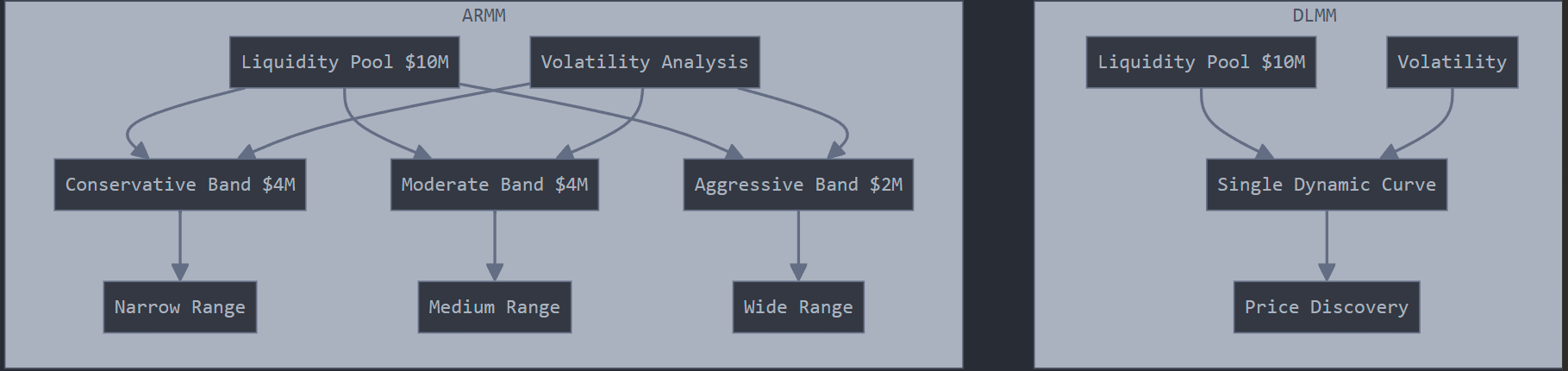
Key Advantages Demonstrated:

1. Capital Efficiency:

   • DLMM: All $10M affected by each market move
   • ARMM: Capital distributed based on market conditions, minimizing unnecessary adjustments

2. Risk Management:

   • DLMM: One-size-fits-all approach
   • ARMM: Different risk profiles handle different market conditions optimally

3. Trading Experience:

   • DLMM: All trades face same conditions regardless of size
   • ARMM: Trades automatically routed for optimal execution

4. Fee Generation:

   • DLMM: Single fee structure must balance all scenarios
   • ARMM: Each band optimizes fees independently, maximizing revenue while maintaining competitiveness

This example shows how ARMM's multi-band approach provides more flexibility, better capital efficiency, and improved risk management compared to traditional DLMM systems. Would you like me to elaborate on any specific aspect of this comparison?

References

[Technical references and citations to be added]

Appendix A: Mathematical Foundations

[Detailed mathematical proofs and models to be added]

Appendix B: Implementation Guidelines

[Technical specifications and deployment considerations to be added]